Graph theory plays a vital role in many fields. The graph concept models many relationships and processes in physical, biological, social, transportation, and information systems. One of the essential fields in graph theory is graph labeling. Graph labeling is widely used in various applications such as coding theory, x-ray crystallography, radar, astronomy, circuit design, addressing of communication networks, database management, etc. In this research, we will examine a form of topology of transportation routes based on graph labeling. The topology of the transportation routes that will be studied is a modified of helm graph. This research aims to determine the total vertex irregularity strength of the modified helm graph denoted by Hn for n≥3. The lower bound is obtained based on the properties of the graph Hn using the existing supporting theorem. The upper bound is obtained by labeling the vertices and edges of the graph Hn in some simple cases. From this labeling, total vertex irregular labeling will be constructed for any n. Based on the results of this research, the total vertex irregularity strength of the graph Hn is 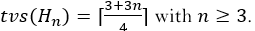

Contact Info
editor@learning-gate.com
For all editorial matters, including decisions on acceptance/rejection and publication status updates.
submissions@learning-gate.com
For submission difficulties, submitting papers via email, and checking submission status.
formatting@learning-gate.com
For assistance with formatting and template-related issues (authors only).
board@learning-gate.com
To request to join or be removed from the editorial board.
support@learning-gate.com
For technical issues or general queries related to the journal website.
This is an open-access article distributed under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License
Licensed under  a Creative Commons Attribution 4.0 International License.
a Creative Commons Attribution 4.0 International License.
 a Creative Commons Attribution 4.0 International License.
a Creative Commons Attribution 4.0 International License.